说明:
傅里叶级数、傅里叶变换、离散傅里叶变换、短时傅里叶变换。。。这些理解和应用都非常难,网上的文章有两个极端:“Esay” Or “Boring”!如果单独看一两篇文章就弄懂傅里叶,那说明你真的是大神了。
本博文是经过查阅网上几十篇大神的博客、文章、书籍等进行的一个汇总,希望对初学者和我自己一个入门和总结,所以本博文并非原创,抄袭+汇总+修改+总结!
主要参考:
1.傅里叶变换到小波变换的风趣讲解:
2.一篇外文的翻译者,讲的非常好,本博文大部分基于此大神的翻译进行的部分优化:
3.风趣幽默的讲解傅里叶的由来和一些基础:
4.网上很多人都基于这篇外文进行的翻译和总结:,外文得FQ,这里下载之后供大家下载:
5.扬州大学的一个PPT讲解傅里叶级数推导,原地址不知道在哪,这里给出好心人上传的百度地址:
6.百度文库关于傅立叶级数到傅立叶变换的详细描述:
7.一位美女大神的博客,貌似还是大四~~
8.参考的博文在这里或者博文结尾给出,文中直接引用将不再进行说明,请见谅!
一.FFT的引出
在上一篇文章我们说到离散傅里叶变换(DFT)-->>“离散信号转化为连续信号,非周期信号转化为周期信号”,这个如果没理解的请看。大家有没有发现一点:DFT只是和你说如何去转化,没有说怎么去计算信号,他所表达的是离散非周期的信号本来是不能计算的,现在我可以把它变换成可以计算的了。那如果你感觉你能轻松的计算出来,就没必要看下面的内容了。
OK~~FFT登场了,它的作用就是快速的计算出来DFT变换之后的信号!
好了,现在引出FFT之后,下面就是介绍FFT原理和实现了。
二.FFT的原理
首先由一个例子切进:
下面是一个多项式函数--->>>
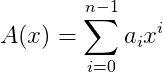
如果我们知道了n次多项式上的n个不同的点,那么这个多项式就可以解出来(高中常识)
这种方法叫做:点值表达

再给出一个多项式:
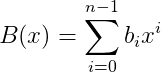
设有2n-2个点:

设:
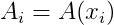 ,
,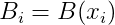
则:
